RF Calculators

  Last Update May 1st 2024


General Issues

---

Frequency to Wavelength

Wavelength Cal. Freq. [MHz]       Velocity Factor [/]       Wavelength λ [m] 1 λ in Vacuum             1 λ in Medium         - - - Common Fractions: 1/4 λ in Vacuum             1/4 λ in Medium         1/2 λ in Vacuum             1/2 λ in Medium         3/4 λ in Vacuum             3/4 λ in Medium

What maths are driving this calculator?

•      Wavelength in vacuum:  λ = c / Frequency

Speed of Light c = 299 792 458 m/s in vacuum

A Wavelength λ in a medium other then vacuum is described by

•      Wavelength λ = (c x Velocity Factor) / Frequency

The Velocity Factor v is a function of as relative dielectrical number or Permittivity of a medium. It describes how fast a wave travels in a medium and thus is directly related to change of length of a wave in that medium.

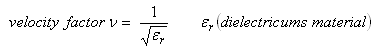
(vacuum)  = 1.00000   =>   v = 1.0000
(air)         = 1.00059   =>   v = 0.9997

Mind that coaxial cables Velocity Factor commonly is given for 1 MHz or so by the manufacturers. Due to a slightly frequency depending of the insulation plastic and hence V-Factor at VHF/UHF cables might be shorter than computed by 4 to 7 percent.

---

EIRP : Equivalent isotropically radiated power

EIRP Calc. Watts at Ant.      Ant. Gain [dBi] EIRP in W          and kW

What is EIRP about?

EIRP is a term often used with the topic of RFI (Radio-Frequency Interference) and Radiation Power of Electromagnetic Fields. Simply put EIRP stands for the equivalent of fed power to an isotropic radiator (gain = 0 dBi per definition) vs. a directional antenna with certain gain over the iso.-radiator and other fed power. By referring to the iso.-radiator directional power levels in beam direction can easily be compared. In Amateur Radio use that could be comparing powers of two stations. Lets assume a DX setup for 432 MHz: one station is feeding 700 W into a 17.1 dBi antenna, the other 400 W into a 19.8 dBi antenna. Which one 'pumps' more radiation power into beam direction?

What maths are driving this calculator?

1. Conversion of Isotropic Gain of Antenna to numeric number

2. EIRP is derived by multiplication of Power in watts with numeric Gain of antenna against an Isotropic Radiator

'Gain,iso' = dBi = dBd + 2.15 dB. Example: 12.10 dBd is 14.25 dBi

---

Watts to dBm & dBm to watts Conversion Calculator

W > dBm W   >     dBm                     dBm > W dBm   >     W

dBm is Decibel-milliwatt, it references power to one mW - with 0 dBm = 1 mW

•    0 dBm = 0.001 W
•  10 dBm =   0.01 W
•  50 dBm =   100 W

What maths are driving this calculator?

---

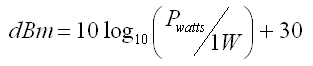
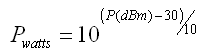
dB Conversion Calculator

Gain, numeric > dB Gain [numeric]   >     Gain [dB] Gain, dB > numeric Gain [dB]   >     Gain [numeric]

This conversion works with GAIN and LOSSES:
• Gain  3.0 dB = 2.00 numeric
• Gain     0 dB = 1.00 numeric
• Gain -3.0 dB = 0.50 numeric

What maths are driving this calculator?

Getting a sense for numeric gain numbers as Power in Watts is multiplied with numeric Gain, see EIRP Calculator:
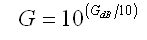
• 2.00 numeric = we know that 3 dB gain gives double output
• 1.00 numeric = adding 0 dB does not change anything
• 0.50 numeric = is half power out

---

Amplification Gain or Attenuation to Watts in/out Calculator

Watts in, Gain or Loss to Watts out Watts input   >     Gain/(-)Loss [dB]         Watts out [W]

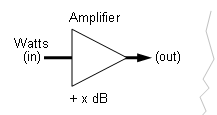
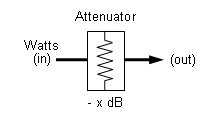
What maths are driving this calculator?

Power Levels in dB can be summed (gain) or subtracted (loss).
So we convert Power Input in watts to Power Level (dB) refering to 1 watt (dBw)

Next we add the Power Levels of fed power and gain or attenuation block

or generalised for any chain of gain and attenuation blocks the formula looks like this:
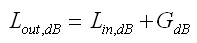
Note the rather explicite notation 'Loss_x'. This commonly would be another G_x with gain < 1.00



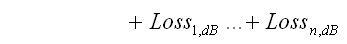
Finally we convert the resulting Power Level (dB) into watts again

---

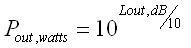
Temperature to dB Calculator

Kelvin to dB Calculator Kelvin [K]         Computed dB or NF

What maths are driving this calculator?

with To = 290 K = 17° Celsius mean ambient temp. (273 K = 0° C)

---

And in reverse ... dB to Kelvin Calculator

dB to Kelvin Calculator dB or NF         Computed Temp. [K]

What maths are driving this calculator?

with To = 290 K = 17° Celsius mean ambient temp. (273 K = 0° C)

---

μV to dBm Calculator

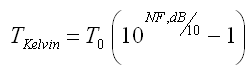
μV to dBm Calculator μV         ohms         Computed dBm

What maths are driving this calculator?

dBm is Power Level referring to 1 mW

---

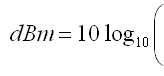
dBm to NF Calculator      Receiver Sensitivity to Noise Figure

dBm to NF Calculator dBm         BW (kHz)         S/N (dB)         Computed dB or NF

• BW = Bandwidth
• dBm = Power Level referring to 1 mW
• To = 290 K or 17° C ambient

Using this calculator with Receiver Specs from a Data Sheets

As different S/N levels are used as well as bandwidth depends, look up those specifications
with the μV or dBm number given for sensitivity and enter to calculator form to yield a correct result

Typical numbers

• nominal BW's: CW or as SSB = from 2.4 ...3 kHz, AM = 6 kHz, FM = 12.5 ... 25 kHz
• CW Filter? => acc. filters bandwidth settings
• nominal S/N = 6, 10 or 12 dB


What maths are driving this calculator?

k = Boltzman's constant (1.3 x 10-23 J/K)

---

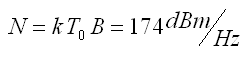
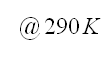
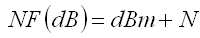
SNR to S-Units and μV Calculator

Enter in dBm IARU Region 1 rec. for Base Level Short Wave = -121 dBm, VHF and up: -141 dBm Base level       Noise Floor       Signal SNR   dB S-Units, absolute    /    plus dB S-Units, relative to noise floor    /    plus dB Volts at 50 ohms   μV

---

G/T Calculator

G/T - Ratio Gain (dBi)         Temp. (K)         Computed G/T (dB)

What maths are driving this calculator?

---

VSWR & Mismatch Loss

Z1 would be Zo or 'at Transmitter or Receiver' while Z2 could be antenna feedpoint impedance

Mismatch Loss (ML) expresses what Losses derive from connecting non similar impedances

VSWR & Mismatch Loss Z1(Ω)         Z2(Ω) = R + j         Z2 absolute        (Ω) VSWR           ( / ) Refl. Coefficient Γ   ( / ) Return Loss    (dB) Mismatch Loss (dB)

Mismatch Loss application example:

Given a 50 ohms feedline coax of 10 m length with a loss of 1.2 dB shall be connected to a 75 ohms antenna. What is the total loss here?

The calculator puts out -0.177 dB for Mismatch Loss, the coax adds 1.2 dB, total loss is 1.377 dB.


What maths are driving this calculator?

Z2 in absolute numbers is

with this we do the rest as follows

---

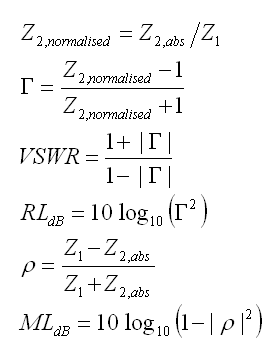
73, Hartmut, DG7YBN