Background Info

Element Diameters and NEC Limitations
Guiding numbers and Limits

Scaling Frequency in Antenna Calc. Programms

Scaling Frequency in 4nec2 and EZNEC

Element Diam. Scaling per Formula by DL6WU / G3SEK

Scaling Element Diameters using a Formula

Element Diam. Scaling by Hand

Scaling Element Diameters by Hand

Step-by-Step Example

Scaling a 50 MHz 5 ele. from 15.875 (5/8 in) to 12.7 mm (1/2 in)



Preface

I am frequently being asked how I scale Yagis to other frequencies or element diameters ...
or whether I could do that on a certain of my designs ... here is a little tutorial how to do that.
Do not get me wrong here, I like to help but it is clear that I can not scale whatever design to
whatever diameter and put it onto the website in the limited time I have ...
So I prefere to give a good instruction to enable other hams to do needed scalings themselfs.

If you would have Brian Brezelys Antenna Optimiser or YO full version it would do it automatically.
But this program is not available anymore and would have to be licensed. And needs some skills
to operate.

News / Update 2015-03-10

Below I show how to scale element by element to new diameter starting with the most far out
directing D x. Recently I found out that with most Long Yagis I am happier starting at the
rear end. Modify the reflector, spare the Driven Element and work towards the last out element
seems to give a cleaner result with less effort to me. That is a subjective measure.
Both ways work but I thought it worthwhile to be mentioned here.

---

Element Diameters and NEC Limitations

The NEC kernels formulas compute to best accuracy with relatively thin wires.
Now what exactly is a thin wire? To give some dirction here I quote the essentail sentences from the NEC II Manual.
The NEC II kernel is used in EZNEC up to the actual version v5.x and in 4nec2 (if no NEC4 kernel is mounted).

Numerical Electromagnetics Code (NEC) . Method of Moments Part III: Users’s Guide,
G. J. Burke, A- J. Poggio, 1981, Lawrence Livermore Laboratory

Section II, Structure Modeling Guidelines
1. wire modeling

      (1) “The main electrical consideration is segment length Δ relative to the wavelength λ.
      Generally, Δ should be less than about 0.1 λ at the desired frequency.“

λ = 2.079 m at 144,200 MHz           0.1 λ =0.1 * 2.079 m = 0.2079 m
A typical 144 Mhz Yagi element may have a length of around 0.998 m;
At a segmentation of 10 per wire the resulting segment length is 0.998 m / 10 = 0.0998 m.
That leads to a minimum to chosen length factor of 0.2079 m / 0.0998 m = 2.08. In straight
words a segmentation of only 10 segm./wire is better than double of the recommended minimum.

As we continue to read down the manual we find the following:

      (2) “[...] while shorter segments, 0.05 λ or less may be needed in modelling critical regions of
      an antenna.”

Taking into account the minimum to chosen length factor we are still on the side of
recommended solution with just 10 segments per wire, even if say the DE to D1 zone of a
Yagi should be considered a critical region.

      (3) “Small values of Δ / a may result in extraneous oscillations in the computed current near
      free wire ends […]. Extremely short segments, less than about 10E-3 λ, should also be avoided […]”.

10E-3 λ = 0.001 λ           0.001 * 2.079 m = 0.002079 m
2.079 m / 0.002079 m = 1000
segment length = Δ , wire radius = a

      “[…] Δ / a must be greater than about 8 for errors of less than 1%.”

Choosing a common diameter for Yagi elements of 8 mm we arrive at a = 8 / 2 mm = 4 mm
Δ / a = 8 gives us a minimum segment length of Δ = 8 * a = 8 * 4 mm = 32 mm.
That equals a maximum segmentation of 998 mm / 32 mm = 31

      “With the extended thin-wire kernel, ? / a may be as small as 2 for the same accuracy.”

Δ / a = 2 gives us a minimum segment length of Δ = 2 * a = 2 * 4 mm = 8 mm.
That equals a maximum segmentation of 998 mm / 8 mm = 124

     “Unless 2 π a / λ is much less than 1, the validity of these approximations should be considered.”

2 π a / λ = 2 π * 4 mm / 2079 mm = 0,0121

Finally lets have a look at how low numbers of segments are used in the NEC manuals examples themselfs.
On the manuals pg. 125 we do find an example of a Yagi – like structure, take a look at the chosen segmentation:

      (4) “Example of a 12 elem. log peridoc antenna
      Total 78 segments, No of Seg/wire 9, 9 ,7 ,7 ,7, 7, 7,5 ,5 ,5 ,5 ,5 ”

OTHER limitations

NEC-2 Manual, part III: User's Guide (WDBN version 0.92), pg. 9:

      "When wires are parallel and very close together, the segments should be
      aligned to avoid incorrect current perturbation from offset match point
      and segment junctions."

EZNEC Manual, s. index for "Wire spacing" or "Closely Spaced Wires"

      "In all cases, wire spacing should be at least several wire diameters."


With wires spaced as closely as 0.01 wl nec2 and nec4 based software produces bad Average Gain numbers.
Numbers for gain and Antenna Temperatures produced with Average Gain numbers far from 1.000 for the lossless model
must be processed through the Average Gain correction formulas, see here

At a distance of 0.025 wl the convergence challenge seems to be cured for most designs.

---

Guiding numbers and Limits

• Making elements thicker we need to lessen their length. Thicker elements are SHORTER
• Making elements thinner we need to extend their length. Thinner elements are LONGER

• Elements are NOT prolonged / shortend in linear way or using fixed numbers over the whole Yagi-Uda.
  While the far out elements need most adaption this flatens out around the driver cell.

An example of what delta length to what element;
note the progression as we move from Driver Cell to far end ...
(50 MHz 5 ele. Yagi from 5/8 to 1/2 in)

Ele.:   Refl    DE     D1     D2     D3
[mm]     1       3      7     17     22


Exemplarily numbers (all strongly depending on actual design)
Band                      50 MHz            144 MHz            432 MHz
                      Refl. /   D5      Refl. /   D10      Refl. /   D10 
 4 mm  <->  6 mm            -            4 mm / 10 mm       3 mm / 7 mm
 6 mm  <->  8 mm            -            4 mm /  8 mm       2 mm / 5 mm     
 8 mm  <-> 10 mm            -                 -                  -
 4 mm  <->  8 mm            -            5 mm / 24 mm            -
 5/8 in - 1/2 in       1 mm / 22 mm           -                  -

It is clear that changing element diameters but leaving element positions as they are leads
to slight changes in distances element-to-element. Thus the Yagi 'never will be the same again' if we
take a macroscopic view by looking at the 10th dB in F/B or F/R or side lobe magnitudes.

Furthermore it is understood that thinner elements introduce more loss and vice versa. So that scaling down
from 8 mm to 6 mm element diameter may cost us 0.05 dB. If it does not this will be on slight cost of other properties
namely F/B or whatever side lobe supression or band width.

---

Scaling Frequency in Antenna Calc. Programms

• 4nec2

This is 4nec2 v5.8.14. The 4nec2 holds a scaling function in the Geometry Editor
First select which wire shall be scaled. I assume all - so use CTRL + A windows shortcut for convenient marking of all wires.
Selected wires turn from blue to red, s. screenshot below

• EZNEC+ v5

EZNEC holds a scaling function that transfers a Yagi or whatever Antenna from given to new frequnecy.
It does not leave the element diameter as it is though.

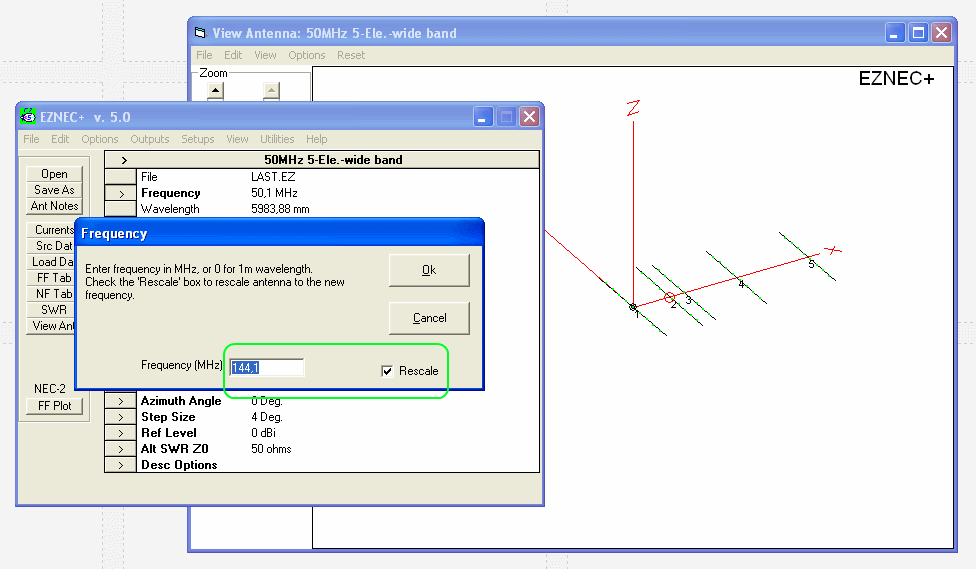
The scaling function does a 100 percent scaling, including the element diameters. We are down from 1/2 in to 4.4158 mm which equals the ratio between 50.1 and 144.1 MHz.

From here on we have to 'adjust' the element diameters to some feasible number like 4 mm, 5 mm or Imperial 3/16 in = 4.763 mm as shown below.
Here click I give an overview on most common Imperial measures to millimeter.

---

Element Diam. Scaling per Formula by DL6WU / G3SEK     2021-10-10

Preface: The following shows a methode for scaling elements to new lengths with a wanted new diameter ar parameter.
This methode is not new. It has been published in the well known VHF/UHF DX Book in 1995 and probably much earlier elsewhere.
I did not introduce this methode on my web until now, since I was never happy with scaling to largly changes of diameters and
in general for longer Yagis from around 10 elements on 70 cm onwards.

Nevertheless I was frequently contacted and asked about this methode. Dan, AC6LA integrated it into his very capable AutoEZ for instance.
Also recently Klaus, DL5AB showed me a quite fine scaling of just the sample design for hand scaling I show down this page.
After a fruitful discussion with him, thanks to Klaus, I decided to not longer hold back this set of formulas and integrated this chapter.
Hand scaling, if done right (hi) leads to better results, but for small changes of diameters on lower bands 144 MHz and below and less
approx. 10 el. it delivers very usable results.

Mind this correction only works for straight elements! A bent dipole, reflector or whatever might come closer if its straightened length
is filled in but still the reactance would not be fully met. Not to mention folded dipoles, quad or LFA loops.

in this

L1		=	Length of source element	mm
D1		=	Diameter of source element	mm
L2		=	Length of scaled element	mm
D2		=	Diameter of scaled element	mm
X		=	Reactance of element	Ω
λ		=	λ = c/f (use f in MHz, c = 299 792.458 mm/s)	mm

A Microsoft TM Excel which makes use of these formulas:

Note that I do not feel responsible for any possible inconventience resulting by making use of this file.
Use this file on your own risk.

Link to download/open this MS Excel:


This Microsoft TM Excel was created by DG7YBN and holds some of the ideas of the file that Klaus, DL5AB showed me.
This Excel computes the impedance of the element as a first stage. This column D is masked.
Of course you can demask it if you like to see those values.

---

Scaling Element Diameters by Hand

I do this by hand. As a preparation I write down three, four key numbers:
Best Return Loss frequency and number in dB, like a Return Loss of -33.4 dB at 432.1 MHz. Then F/B and Gain.

For adjusting element lengths to a new diameter I start with the farest out parasitic Element.
Set this one to new diameter only. Modify length so that F/B and Return Loss are similar to before.
Then modify next inner parasitic element moving toward the Driven Element. Same routine, next element,
same routine ,....., DE, same routine, finally Refl., same routine

Note: 1. The Refl. demands the least change in length of all (some have next to none change of length on the Refl, depending on design!),
Farest out parasitic ele. or second farest have most change in length. From Farest out Dxx length change
decreases until very little delta length for DE and Reflector only.

2. Gain will suffer by some 0.05 dB or so when moving to thinner elements due to higher losses.
Some way gain will increase a little for thicker elements.

3. F/B can not stay absolutely same, for this is a close similar antenna now, but not absolutely identical.
Why? The ratio of absolute distances between elements (i.e. ele. positions from ele. to ele. surface have
changed slightly simply because they are thicker / thinner now.)

4. Thicker ele. are shorter / Thinner ones longer.

---

Scaling a 50 MHz 5 ele. from 15.875 (5/8 in) to 12.7 mm (1/2 in)

How to scale a Yagis elements one-by-one by hand:
Starting with the farest out parasitic element working towards the DE and finally adjusting the Refl.

• 1. Writing down F/B, Gain and SWR at a distinctive point
Elevation and SWR plot of our unscaled Yagi. Key properties of our starting point Yagi with 5/8 in elements are

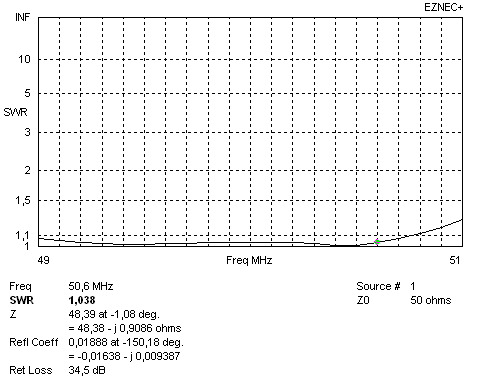
Forward  Gain    9.91 dBi
F/B             25.49 dB
Return Loss    -34.5  dB at 50.60 MHz as a distinctive point

• Scaling D3
Modifying D3's diameter to 1/2 in leads to

which leaves us with an F/B of 23.96 dB instead of original 25.49 dB

Lengthening D3 millimeter by millimeter working towards same F/B as before leads to F/B of 25.46 dB at a new length of 1236 mm / side.
Forward Gain is back from 9.86 dB to 9.91 dB too.

Time to check in the SWR Plot window => With new D3 diameter we find a Return Loss of -34.5 dB at our mark of 50.60 MHz.
Note that the only parameter I was adapting to was F/B and still the Return Loss and complete RL plot are fine now.
Good enough ... , now up to next element in row

• Scaling D2
Modifying D2's diameter to 1/2 in leads to

which leaves us with an F/B of 26.25dB instead of original 25.49 dB

Lengthening D2 millimeter by millimeter working towards same F/B as before we can see how the F/B lessens with
every added millimeter until we arrive at same F/B as before.
At a new length of 1328,4 mm oer side we find an F/B of 25.49 dB and Forward Gain is back to 9.91 dB too.

and pattern as with all 5/8 in elements

and finally verifying the SWR or Return Loss plot; yet again, our marker at 50.60 MHz shows almost same result:
we started with an RL = 34.5 dB and now have a 35.2 dB. Yet again, all achieved by using the F/B as trimming param only.

• Scaling D1
Modifying D1's diameter to 1/2 puts it all to a test since D1 is very responsibly for Z and the Return Loss plot ..

and indeed we are not far off ... RL(50.60 MHz) = 32.0 dB against -34.5 dB at starting point

and this is the point were we see the finite accuracy when scaling element diameters while
element positions are fixed. With 0.2 mm less lenght on D1 we come closer to the RL as was
but drift away slightly from the original F/B. With constant element positions there is no choice
but to arrange an intermediate arrangement.

So I draw back the lenght of D1 from the just found 1379.7 mm to 1379.5 mm.

• Scaling the DE
Modifying DE's diameter to 1/2 in we split from the 'tune it to similar F/B dogma' and adjust Z with
an eye on the imaginary part jX in the Z = R + jX until Return Loss plot and our marker are quite close to
the starting point once again

I get an RL(50.60 MHz) = -33.4 dB for a new length of 1469.5 mm each side.

• Scaling the Reflector
Modifying the Reflectors diameter to 1/2 we find that it does not have to be modified at all.

Finally check the pattern and SWR plot ... still same .. almost

finished ...

---

73, Hartmut, DG7YBN